1、测量

1）测量依据:JJ G—1999《弹簧管式精密压力表及真空表》检定规程;JJ G59 —1990《二、三等标准活塞式压力计》检定规程。

2）环境条件:温度 20.5 ℃。

3）测量标准:二等活塞压力计 ,测量范围: 0～60)MPa ,允许误差: ±5 ×10-4读数值。

4）被测对象:0.4 级 ,测量范围 0～10 MPa 精密压力表。

5）测量方法:依据检定规程对精密压力表的检定是应用直接比较法 ,由二等活塞压力计产生的压力与精密压力表指针所指示的压力相等来完成在活塞压力计上加上相应的专用砝码 ,当砝码作用于活塞有效面积所产生的标准压力与造压器发生的压力相平衡时 ,被检精密压力表指示值与标准器产生的标准压力值之差值即为精密压力表的示值误差。

2、数学模型

2.1建立数学模型

Δp = p _x - p _n              (1)

式中: Δp 为被检精密压力表的示值误差,单位为MPa; p_x为被检精密压力表的实际指示值,单位为MPa; p_n为用专用砝码加载于活塞压力计上产生的标准压力值,单位为 MPa。

2.2 　灵敏系统

对式(1)微分得灵敏系数: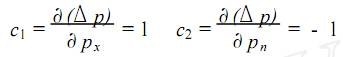

 

3、测量不确定度来源

3.1精密压力表引起的标准不确定度分量

1)重复测量引起的标准不确定度分量;

2)估读引起的标准不确定度分量;

3)环境温度引起的标准不确定度分量。

3.2标准活塞压力计引起的标准不确定度分量

1)活塞压力计量传时引起的标准不确定度分量;

2)活塞下端面与精密压力表指针轴之间的高度差影响引起的标准不确定度分量。因为选用的精密压力表为 0～10 MPa,根据检定规程,液柱高度差影响可以忽略不计。

4、入量的标准不确定度评定

4.1被检精密压力表引起的标准不确定度分量 u

1)精密压力表示值重复测量引起的标准不确定度分量 ux1

为了获得重复性测量的标准不确定度,用二等标准活塞压力计对精密压力表 10MPa 点进行 10 次连续重复独立测量 ,得到测量列:10. 005 ,10. 005 ,

10.005 ,10. 005 ,10. 010 ,10. 010 ,10. 010 ,10. 010 ,

10.010 ,10.010。

测量结果平均值:

MPa

单次测量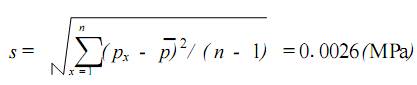标准差:

 

平均值标准差: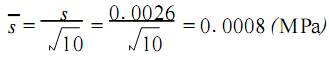

 

重复测量的平均值标准差即为重复测量的标准

不确定度

Ux1=0.0008(MPa)

自由度V x1= n - 1 =9

2)被检精密压力表估读引起的标准不确定度分量 u x2B 类标准不确定度

实际检定时,精密压力表的估读误差为最小分度值的 1/ 10,014 级、0～10 MPa 精密压力表,其估读误差为01005MPa,误差分布服从均匀分布,则包含因子 k = √3。

u _x2=0.005/√ 3 =0.0029 MPa

估计其不可信度为10 %,则自由度为:

 

3)环境温度引起的标准不确定度分量 u _x3(B类标准不确定度)

因检定温度在检定环境温度 20 ±3 ℃范围内,温度引起的标准不确定度分量可以忽略不计。

因各不确定分项 u _x1、u _x2 、u _x3彼此独立,互不相关,由合成标准不确定公式得

 

4.2 　标准活塞压力计引起的标准不确定度分量 u2

二等标准活塞压力计检定 10MPa 点的允许误差为 a = ±0.05 % ×10 = ±0.005MPa。取 a 的半宽为 0.005MPa ,误差服从均匀分布 ,则包含因子k= √3。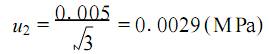

 

估计其不可信度为 10 %,故自由度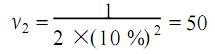

 

5合成标准不确定度的评定

5.1合成标准不确定度 u c的计算

因输入量 p x 和 p n彼此独立,互不相干,所以合成标准不确定度可按下式求得:

∵c =1,c = - 1

 

5.2　合成标准不确定度 u 的有效自由度 的计算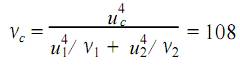

 

V eff=Vc=108

6 　扩展不确定度的评定

取置信概率 p =95 %,按有效自由度V eff =108,

查 t 分布表得:k 95=1.984。扩展不确定度

U95= k 95·u c =1.984 ×0.0042 =0.008 (MPa)

7 　测量不确定度报告

用二等活塞压力计检定 0.4 级、测量范围 0～10 MPa 精密压力表的 10MPa 点,其测量结果为10.008MPa,测量结果扩展不确定度为:

U95 =0.008MPa, V eff=108 电磁流量计 测温枪 压力变送器